Various Forms of the Equation of a Line
Various Forms of the Equation of a Line: Overview
This Topic covers sub-topics such as x-intercept and y-intercept of a Line, Equation of Straight Line in Intercept Form, Equation of Straight Line in Two Points Form and, Equation of Straight Line in Slope Intercept
Important Questions on Various Forms of the Equation of a Line
Find the equation of a straight line which is parallel to the line and passes through the point
A straight line cuts the co-ordinate axes at and If the mid-point of is find the equation of
A straight line cuts the co-ordinate axes at and . If the midpoint of is , find the equation of .
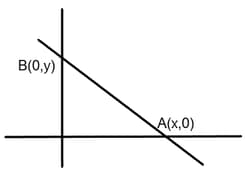
A straight line cuts the co-ordinate axes at and . If the midpoint of is , find the equation of .
Write the equation of the lines for which , where is the inclination of the line and -intercept is .
Show that two lines and , where are perpendicular if .
Equation of a line is . Find its -and -intercepts.
Equation of a line is . Find its slope.
The slope of a line joining the points and is then find
The equation of right bisector of the line joining the points and is
Let be three points then the equation of bisector of the angle is
A straight line whose slope is passes through the point and intersects in distinct points. Hence lies in the interval
Find the equation of line at which the length of the perpendicular from the origin is and the slope of this perpendicular is
Let a line cuts an intercept of units and units on positive sides of axes. Find the number of integral values of so that the coordinate of the point of intersection of lines and is also an integer.
The angle between the lines and -axis is
A line is such that its segment between the lines and is bisected at the point . Obtain its equation.
Find the equation of a line perpendicular to the line and passing through the point .
Reduce the equation into normal form. Find the values of and .
Find the equation of the line whose perpendicular distance from the origin is units and the angle which the normal makes with positive direction of -axis is .
The Fahrenheit temperature and absolute temperature satisfy a linear equation. Given that when and that when . Express in terms of and find the value of , when .
